It has become almost a truism in critical examinations of the Blogosphere to talk about how – with the explosion in weblog numbers – it becomes difficult to find the best insights on any given subject. I first came into contact with the clear expression of this idea in an article called Scaling Clay Shirky but it’s recently been pretty much everywhere…
I believe that there are some legitimate concerns in these sentiments, but I think fundamentally they miss the point – it’s my opinion that replication of content online and a massive increase in the number people posting about a specific issue does not constitute a problem for the blogosphere, but instead one of its most significant advantages. In fact I’d go further and say that where there are problems, these can be resolved by simply speeding up the self-organising mechanisms that are implicit within the blogosphere, which is, I think what sites like Daypop, Blogdex, Popdex and Technorati are currently doing, albeit in a reasonably primitive way. But I’m getting ahead of myself. Today I’m just going to talk about How do we reach 100% information saturation on any given subject in the blogosphere without reading anywhere near 100% of the weblogs in it? Or to put it another way: With everyone posting lots, does the system help me find the good stuff?
- Before I start though – here’s a simplified, and easier to assimilate / read pdf version of what I’m about to say: scaling_clay_shirky.pdf [75k]
Let’s start off by aggregating all the possible insights about a given subject from all the weblogs that specifically refer to it. This total aggregation will represent 100% of the information available on the subject in the blogosphere at a point in time.
If information was distributed evenly throughout webloggery and weblogs were read randomly then take-up of information would be linear and stable – in order to get 100% of the insights, you’d have to read 100% of the weblogs.

[In this first graph I’ve plotted on the left the amount of information that you’ve managed to assimilate versus (on the right) the percentage of the weblogs that you’d have to read in order to get that amount of information – in the very specific special case that information is distributed evenly and randomly. The features of this “special case” will gradually be removed over the rest of the article. Another point I should perhaps clarify is that I’ve tried to conceive of the bottom axis as also including the order in which one reads the weblogs – that should become clearer through the article…]
However, we know it to be the case that information will not be distributed evenly throughout these weblogs. Many weblogs will contain limited information of any kind. Some will contain a lot. Many will contain replicated information that could easily be found on other sites.
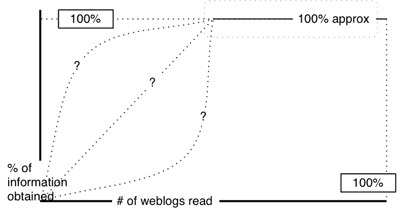
In this graph, ignore for the moment the dotted lines on the left. they represent nothing but the uncertainly fo the beginning of the curve. This diagram takes into account that weblogs have different levels of insight withint them, and that information is often replicated (either by active memetic spread or because the insights are simple and common). In the vast majority of cases then – even given that you’re still reading weblogs in a totally arbitrary order – it’s likely that you’ll get extremely close to the 100% saturation point a significant way before you’ve read 100% of the available weblogs.
In practice – again assuming that you were reading the weblogs in a random order, it would be impossible to gauge the particulars of the curve that led up to the near-as-dammit-to-100% information saturation point. A sample curve would probably be organised in a series of steps – with gradual accretion of insight being the normal, but with occasional significant massive leaps also occurring.
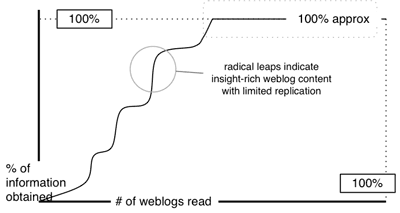
Now – all these models have been based upon the assumption that the order in which the weblogs are read will be random. In fact nothing could be further from the truth. Some weblogs are clearly more likely to be read – this is not necessarily purely based upon the value of their contributions, but it’s not completely distinct from such valuations either. It would probably be fair to say that on average well-linked-to sites are more likely (albeit perhaps only incrementally) to contain insight than sites which are not linked to at all. Secondly, if someone does produce content of value and insight on any specific subject, then it is more likely to be linked to – which in turn increases the likelihood that an individual will visit the site in question.
Both of these criteria suggest that (in our attempts to reach the 100% insight threshold) we will be more likely to be initially directed to high-insight sites than low-insight sites. This changes our graph substantially.

It seems likely, in other words, that even if there’s a limited tendency for sites with more insight to be read first – then the information accretion would be remarkably steep initially and the level off dramatically close to the 100% saturation point.
Hypothetical conclusions: For any given body of information on weblogs, no matter the rate of replication of information or the number of people who post exactly the same comments, close to 100% of the available insight can be reviewed by reading a disproportionately small number of sites – sites that will – as a rule – be among the first that they stumble across through their normal browsing and research patterns.
Related Hypotheses perhaps worth exploring: (1) The larger the number of posts about a subject (and hence the more likely replication) the smaller the proportion of those sites that need to be read in order to have reviewed close to 100% of the available insight. (2) The size of the available insight will increase as the number of posts about a subject increases (although perhaps not in linear proportion).